微分
符号微分:直接使用链式法则对表达式求导。优点是数值精确,缺点为表达式膨胀
数值微分:使用有限差分求解:
数值微分会由于计算机中不同浮点数精度(FP16, FP32,
FP64)而造成截断误差(truncation error)和舍入误差(round-off
error)
自动微分:
- 所有数值运算都由有限的基本运算构成
- 基本运算的导数表达式已知
- 通过链式法则链接将数值计算各部分组合为整体
自动微分中的 表达式追踪(Evaluation trace) 能追踪数值计算过程中的中间变量。以下述函数为例
表示为计算图为
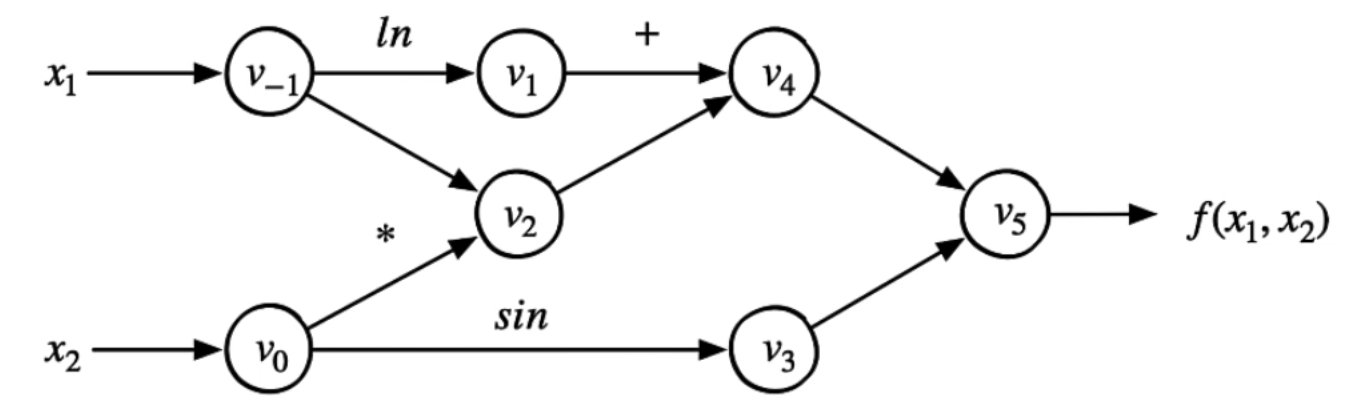
前向微分 (forward mode)
从输入出发,逐步使用链式法则进行求导。

- 通过一个输入可以求解所有的输出微分,不适用与深度学习多输入少输出的情况
后向微分 (backward mode)
对于每一个结点,求解最终输出对该结点的导数。注意每一次求导需要用到后继相邻结点的导数。

- 可以一次性求解所有输入的微分,但需要大量存储空间存储中间结果的微分
Jacobian 矩阵
前向和后向微分都可以使用 Jacobian 矩阵来表示:对于函数
称为原函数的 Jacobian 矩阵。其中每行为后向微分 (Adjoint) 的求解结果,每列为前向微分 (Tangent) 的求解结果。
- 输出数量小于输入时,常用后向微分方法;反之前向。
自动求导实现方法
- LIB:基本表达式,封装基本的表达式及其微分表达式作为库函数,运行时记录基本表达式和相应的组合方式,使用链式法则对基本表达式的微分结果进行组合
- OO:操作符重载,利用语言多态,使用操作符重载基本表达式运算符,其余类似LIB,代表库为
PyTorch - AST:源码转换,语言预处理、编译器或解释器的扩展,对程序表达进行分析得到基本表达式的组合方式,代表库为
MindSpore