HPC | Modern Architecture-Cache

(Updated: )
HPC3

Parallel Programming: Concepts and Pracitce - Chapter 3

von Neumann bottleneck: 现代微处理器能够以远高于从主存（DRAM）中读取数据的速率处理数据。 导致的结果是，很多程序受限于访存，而非计算。当然，现在也有很多访存友好的算法， 例如 BLAS 库中的 GEMM

缓存算法

缓存算法主要解决以下问题：

  • 我们需要从主存装载哪些数据，储存在何处
  • 缓存已满时，我们需要移出哪些数据

缓存算法的目的在于优化其 命中率（cache hit）。算法遵循以下两条原则：

  • 空间局部性：许多算法会从连续的内存位置访问数据，有较高的空间局部性。例如如下程序：
1
2
3
for (int i = 0; i < size; i += 1) {
    max_value = max(a[i], max_value);
}

起始缓存为空，访问 a[0] 时缓存未命中，需要载入数据，缓存一般一次载入一个完整的 cache line。 假设 cache line 大小是64B，数组的值是双精度浮点数（float64），则连续的8个值 a[0:8] 会一起被载入缓存， a[1:8] 的数据全部缓存命中。

  • 时间局部性：缓存被组织为一定数目的块，即 cache line。每个块有固定的大小。缓存映射策略可以决定主存的一个特定条目的备份在缓存中的存储位置。
    • 直接映射缓存 direct-mapping cache：主存每个特定条目在缓存中有唯一的存储位置。命中率较低。
    • 2路组相联缓存 two-way set associative cache：从主存载入的数据可以存储在2个可能的块中，具体存储的位置由 最近最少使用（least-recently used, LRU） 原则决定，往往会选择最近时间最少使用的那个块用来存储主存载入的数据。命中率高于直接映射。常用的还有4路、8路等。

缓存一致性

假设需要修改缓存中的值，则不仅需要修改缓存中的值，还需要修改主存中的值，不然会产生不一致（inconsistency）， 有两种策略去保证缓存和主存中的一致性（coherence）：

  • 直写式：如果主存中的数据已经缓存，则主存数据发生变动的同时也要修改缓存的值。缺点每次写主存需要一次主存访问
  • 回写式：缓存的值修改时，不会立马修改主存的值，而是会被标记为 dirty，待数据移出缓存时，才写入主存

多级缓存和多核处理器的情况会非常复杂，例如每个处理器有自己的本地缓存L1，同时所有的处理器又共享一个公共缓存L2，每个处理器修改L1时，如果没有约束条件，可能会导致其它处理器缓存的值与修改后不一致，L1的值与L2的值也不一样。

一种方式是对于缓存且被修改的值，让其它处理器标记该数据的缓存行为失效，除非重新从主存中载入数据。常用的协议有MESI协议。

虚假共享：缓存一致性协议是对于 cache line 而言的，每一行能存多个值，如果修改了某个值，其所在的 cache line 以及其所关联的 cache line （其它核心的 cache line）将会整体失效。一个极端情况是，多个处理器同时修改一个缓存行的不同数据，任意一个写操作都会使缓存行失效，所有处理器都需要从共享主存重新载入数据，即使数据并没有改变。这种情况就是 虚假共享。

对于程序员的准则：

  • 避免对存储在同一个缓存行中的条目进行过度更新
  • 尽量在寄存器而不是在缓存中存储中间结果

如果数据没有被缓存，则数据仍然需要从主存中缓慢地传送出来，其访问时间在CPU或者GPU上会高达几百个时钟周期，解决的方式有

  • 并发多线程技术 simultaneous multi-threading, SMT：在多个线程之间快速切换，用计算时间掩盖访问时间
  • 硬件预取技术 hardware prefetching：在能预先知道处理器需要的数据时，在使用这些数据前通过硬件（目前也可由程序员自行编程实现）提前将其装载在缓存中

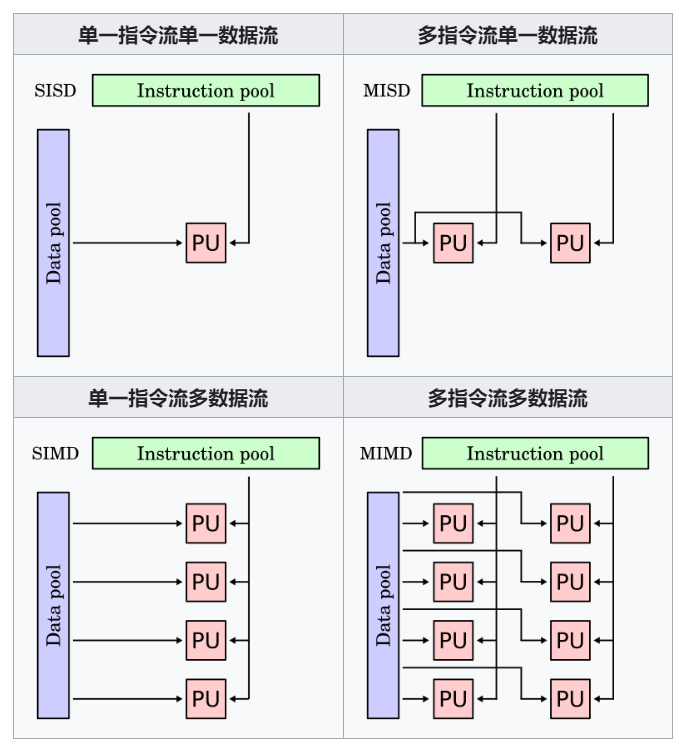
Flynn分类法

将处理器的并行性根据体系结构的指令和数据流分为4种类型：

Flynn Taxonomy
  • SISD：即传统的 von Neumann 体系结构，单个串行的处理单元操作单个数据
  • SIMD：在多个数据上并发地执行同一个操作
  • MIMD：多个处理单元在多个数据上进行不同的指令
  • MISD：多个处理单元在单个数据流上执行不同的指令，并行性少见，但可用于流水线体系结构

现代CPU和GPU在不同层次上的并行：

  • 多重核心：集成一定数量的核心（或者多处理器构成的流水线），能异步独立执行多个线程，现代微处理器使用MIMD并行
  • 向量单元：基于每个处理器上的SIMD向量单元实现数据并行性，例如512位的向量单元可以并行执行16对单精度浮点数的加法操作
  • 指令级并行：通过指令流水线和超标量执行实现

SIMD：在每个时钟周期，通过向全体可用的处理单元（Processint Element, PE）或者计算逻辑单元（Arithetic Logical Unit, ALU）分发相同的指令，SIMD体系结构实现数据并行（data parallelism）机制。因此该体系结构只需要一个单独的控制单元。例如对于简单的向量逐元素相减：

1
2
3
for (int i = 0; i < n; i += 1) {
  w[i] = u[i] - v[i];
}

由于循环中的每个迭代都是独立且规则的，考虑n个ALU在单独控制单元下运行，只需要将向量的每个元素u[i], v[i]放入对应的寄存器U, V，再执行简单的减法操作U-V，ALU[i]便能计算出对应的值w[i]。 但并非所有算法都对SIMD友好，例如在循环中加入条件语句：

1
2
3
4
5
6
7
for (int i = 0; i < n; i += 1) {
  if (u[i] > 0) {
    w[i] = u[i] - v[i];
  } else {
    w[i] = u[i] + v[i];
  }
}

为了将带有条件语句的for语句映射到SIMD体系结构上，需要允许ALU存在idle状态，即跳过一次计算，此时上述代码可以分为三步进行数据并行：

  1. 判断向量u各个元素与0的大小并标记对应的ALU是否执行第1个条件语句块，是则非idle状态，否则为idle状态
  2. 非idle状态的ALU执行语句
  3. 反转各ALU的idle状态，执行语句

在x86架构上已经可以使用SSE（流式SIMD扩展）进行向量计算。通过AVX（Advanced Vector Extension），可以使用内联函数（intrinsic）开发向量寄存器。可以实现下面程序，测试普通矩阵乘法、转置矩阵乘法和AVX转置矩阵乘法之间的性能差距：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include <chrono>
#include <corecrt_math.h>
#include <cstdint>
#include <intrin.h>
#include <iostream>
#include <stdint.h>
#include <stdlib.h>
#include <vector>

// #include "include/hpc_helpers.hpp"

#define TIMERSTART(label)                                                      \
  std::chrono::time_point<std::chrono::system_clock> a##label, b##label;       \
  a##label = std::chrono::system_clock::now();

#define TIMERSTOP(label)                                                       \
  b##label = std::chrono::system_clock::now();                                 \
  std::chrono::duration<double> delta##label = b##label - a##label;            \
  std::cout << "# elapsed time (" << #label << "): " << delta##label.count()   \
            << "s" << std::endl;

#define PRINT_MATRIX(mat, row, col)                                            \
  for (int i = 0; i < row; i += 1) {                                           \
    for (int j = 0; j < col; j += 1) {                                         \
      std::cout << mat[i * col + j] << " ";                                    \
    }                                                                          \
    std::cout << std::endl;                                                    \
  }

// If the matrices are too huge, don't use this function
void SISDNaiveMatrixMult(std::vector<float> a, std::vector<float> b,
                         std::vector<float> &c, const uint64_t row_a,
                         const uint64_t col_a, const uint64_t row_b,
                         const uint64_t col_b) {
  if (col_a != row_b) {
    std::cout << "Shape error, two matrices can't be multiplied." << std::endl;
    return;
  }
  TIMERSTART(SISD_naive_mm)
  for (uint64_t i = 0; i < row_a; i += 1) {
    for (uint64_t j = 0; j < col_b; j += 1) {
      float accum = 0;
      for (uint64_t k = 0; k < col_a; k += 1) {
        accum += a[i * col_a + k] * b[k * col_b + j];
      }
      c[i * col_b + j] = accum;
    }
  }
  TIMERSTOP(SISD_naive_mm)
}

// Transpose matrix b firstly, and then do multiply
void SISDTransposeMatrixMult(std::vector<float> a, std::vector<float> b,
                             std::vector<float> &c, const uint64_t row_a,
                             const uint64_t col_a, const uint64_t row_b,
                             const uint64_t col_b) {
  if (col_a != row_b) {
    std::cout << "Shape error, two matrices can't be multiplied." << std::endl;
    return;
  }
  std::vector<float> bt(b);
  TIMERSTART(SISD_transpose_mm)
  TIMERSTART(SISD_transpose)
  for (uint64_t i = 0; i < row_b; i += 1) {
    for (uint64_t j = 0; j < col_b; j += 1) {
      bt[j * row_b + i] = b[i * col_b + j];
    }
  }
  TIMERSTOP(SISD_transpose)

  TIMERSTART(SISD_mm)
  for (int i = 0; i < row_a; i += 1) {
    for (int j = 0; j < col_b; j += 1) {
      float accum = 0;
      for (int k = 0; k < col_a; k += 1) {
        accum += a[i * col_a + k] * bt[j * row_b + k];
      }
      c[i * col_b + j] = accum;
    }
  }
  TIMERSTOP(SISD_mm)
  TIMERSTOP(SISD_transpose_mm)
}

void SIMDTransposeMatrixMult(std::vector<float> a, std::vector<float> b,
                             std::vector<float> &c, const uint64_t row_a,
                             const uint64_t col_a, const uint64_t row_b,
                             const uint64_t col_b) {
  if (col_a != row_b) {
    std::cout << "Shape error, two matrices can't be multiplied." << std::endl;
    return;
  }
  std::vector<float> bt(b);
  TIMERSTART(SIMD_transpose_mm)
  TIMERSTART(SIMD_transpose)
  for (uint64_t i = 0; i < row_b; i += 1) {
    for (uint64_t j = 0; j < col_b; j += 1) {
      bt[j * row_b + i] = b[i * col_b + j];
    }
  }
  TIMERSTOP(SIMD_transpose)
  TIMERSTART(SIMD_mm)
  for (uint64_t i = 0; i < row_a; i += 1) {
    for (uint64_t j = 0; j < col_b; j += 1) {
      auto accum = _mm_setzero_ps();
      // 128 bit, 4 float32
      for (uint64_t k = 0; k < col_a; k += 8) {
        auto ai = _mm_loadu_ps(&a[i * col_a + k]);
        auto bi = _mm_loadu_ps(&bt[j * row_b + k]);
        accum = _mm_add_ps(_mm_mul_ps(ai, bi), accum);
        auto ai2 = _mm_loadu_ps(&a[i * col_a + k + 4]);
        auto bi2 = _mm_loadu_ps(&bt[j * row_b + k + 4]);
        accum = _mm_add_ps(_mm_mul_ps(ai2, bi2), accum);
      }
      c[i * row_a + j] = accum[0] + accum[1] + accum[2] + accum[3];
    }
  }
  TIMERSTOP(SIMD_mm)
  TIMERSTOP(SIMD_transpose_mm)
}

int main() {
  const uint64_t row_a = 1 << 11;
  const uint64_t col_a = 1 << 11;
  const uint64_t row_b = 1 << 11;
  const uint64_t col_b = 1 << 11;
  std::vector<float> a(row_a * col_a, 1.);
  std::vector<float> b(row_b * col_b, 1.);
  std::vector<float> c(row_a * col_b, 0.);
  // SISDNaiveMatrixMult(a, b, c, row_a, col_a, row_b, col_b);
  // SISDTransposeMatrixMult(a, b, c, row_a, col_a, row_b, col_b);
  SIMDTransposeMatrixMult(a, b, c, row_a, col_a, row_b, col_b);
  return 0;
}

上述程序的输出为（i7-11800H）：

1
2
3
4
5
6
7
# elapsed time (SISD_naive_mm): 174.542s
# elapsed time (SISD_transpose): 0.0413579s
# elapsed time (SISD_mm): 44.8414s
# elapsed time (SISD_transpose_mm): 44.8848s
# elapsed time (SIMD_transpose): 0.0398632s
# elapsed time (SIMD_mm): 15.4761s
# elapsed time (SIMD_transpose_mm): 15.5185s