Parallel Programming: Concepts and Pracitce - Chapter 1
概念
加速比
Speedup:衡量一个并行算法比串行算法快多少的指标。即使用单个处理器运行程序所花费的时间
通常我们希望得到的加速比为线性加速比,即用
效率
Efficiency:定义为加速比和处理器数目之比,衡量了平均一个处理器带来的加速比。当效率为
可扩展性 Scalability:分为强可扩展性和弱可扩展性。
- 强可扩展性 Strong Scalability:测量效率时仅改变处理器的数目,输入数据的规模保持不变
- 弱可扩展性 Weak Scalability:处理器的数目随着输入数据规模共同变化(处理器数目翻倍时,测量效率时把数据规模也翻倍)
计算通信比 Computation-to-communication Ratio:定义为计算花费的时间和处理器间处理消息通信花费的时间之比。
分布式内存系统:每个计算单元只能访问自己的本地内存,如果需要访问其它单元,需要通过一个显式的通信步骤(例如通信网络)实现。
共享式内存系统:所有计算单元共享内存,除此之外,自己本身也有更小的内存(分级缓存)。
并行程序设计时需要考虑划分(数据并行、任务并行、模型并行)、通信、同步和负载平衡等。
求和的例子
现在我们进行一组数据的加法求和操作,其中数据量为
- 数据分发次数:
- 每个处理器本地求和:
- 每个处理器将结果传递给一个处理器(数据收集):
- 中间结果求和:
总的求和运行时长为
其加速比为
对于固定的
因此在固定数据规模和处理器数量时,要提高加速比,需要降低计算通信比。同时,加速比也可以是处理器数量的函数:
令偏导为
综上所述,有如下规律:
- 当数据规模固定时,加速比依赖于采用的计算单元的数目和计算通信比
- 通常情况下,加速比随着计算单元的增加达到局部最大,但使用更多计算单元时,加速比会降低
- 最优的加速比依赖于计算通信比,通信时长占比越大,使用的计算单元数目应该越少
前缀和的例子
前缀和问题:现有
- 输入:一个二元可结合运算符
; 个待运算的数据 - 输出:
个数据 ,其中对于
由于计算
- 数据划分:使用 分治 策略,将
个数据按顺序均分为 份,分别分给 个计算结点,每个结点计算本地内存的前缀和,花费的时间为 - 数据归并:递归 合并相邻的结点数据,即左边结点将前缀和的 最后一个结果 返回,传递给右边结点,右边结点接收左边的前缀和,并将其与自己结点结果求和
- 所有线程将结果返回,计算完成
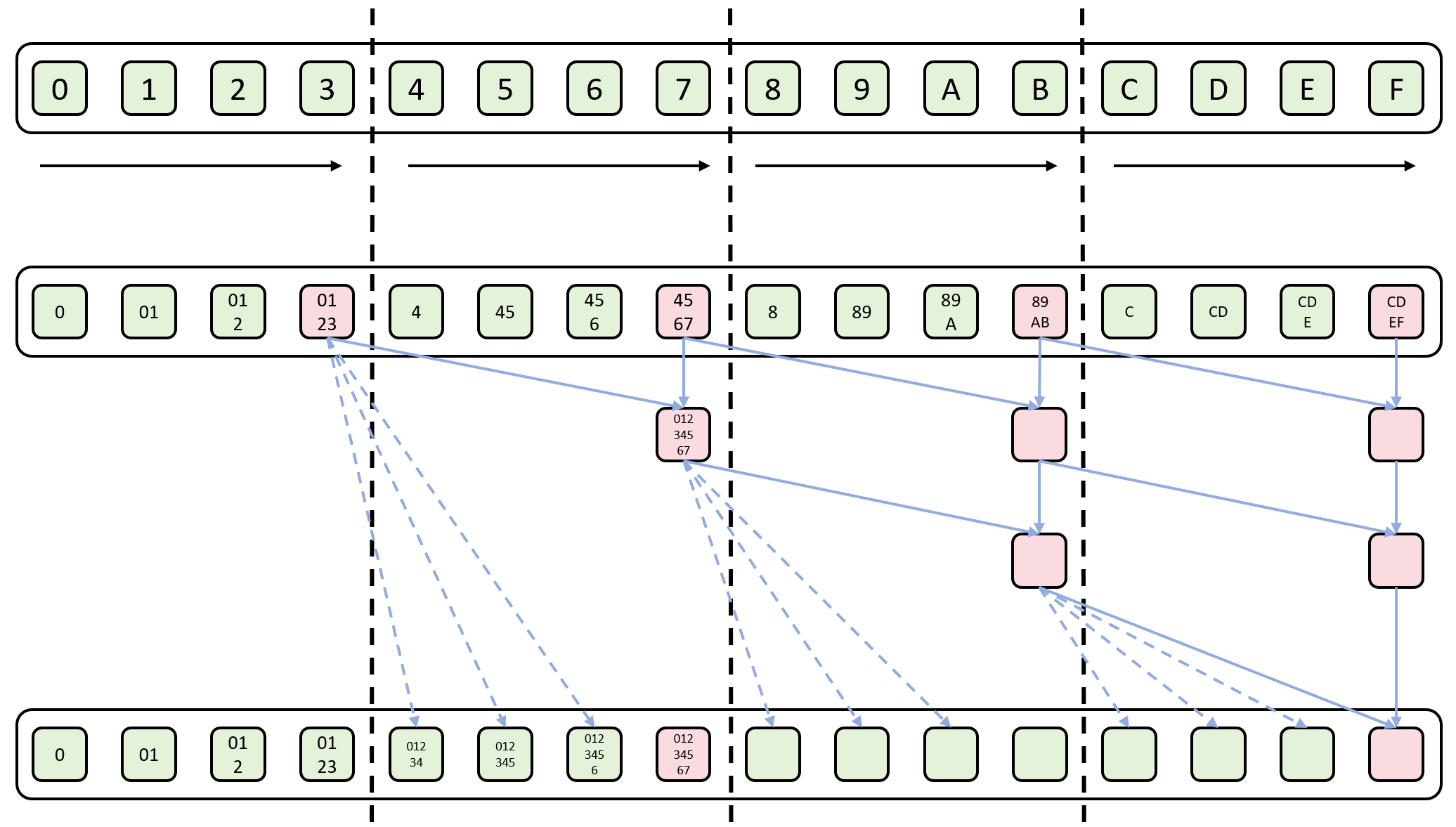
前缀和问题将在后续进行更加详细的讨论。